With common core some people love it and other people hate it. I fall into the camp of people that love it. Before those of you who hate common core write me off a delusional let me tell you why. I enjoy that common core shows another method for students who do not understand under the traditional method and one of the methods that I particularly like is Lattice Multiplication. I will help you learn this method by taking you through Lattice Multiplication step by step.

*This post may contain affiliate links for full disclosure click here.

What Is Lattice Multiplication?

Lattice multiplication is a more visual method of multiplication. It sets up the multiplication problems within a grid. The smallest normally used is a two by two grid (which I will be focusing on), but it can be expanded to multiply bigger numbers as well. This grid functions much like a multiplication table.

Why Teach Lattice Multiplication?

The reason I love common core is that it really helps the students who do not understand in the traditional method. Some students need something that is more visual to be able to get how to do the problem. This is especially true of high functioning special needs students. Lattice Multiplication also takes out the need to put a placeholder, which in my experience many students can forget to do.

For someone who is used to the traditional method this method may be daunting but don’t worry I will break it down for you step by step here.

Lattice Multiplication Step By Step: Step 1

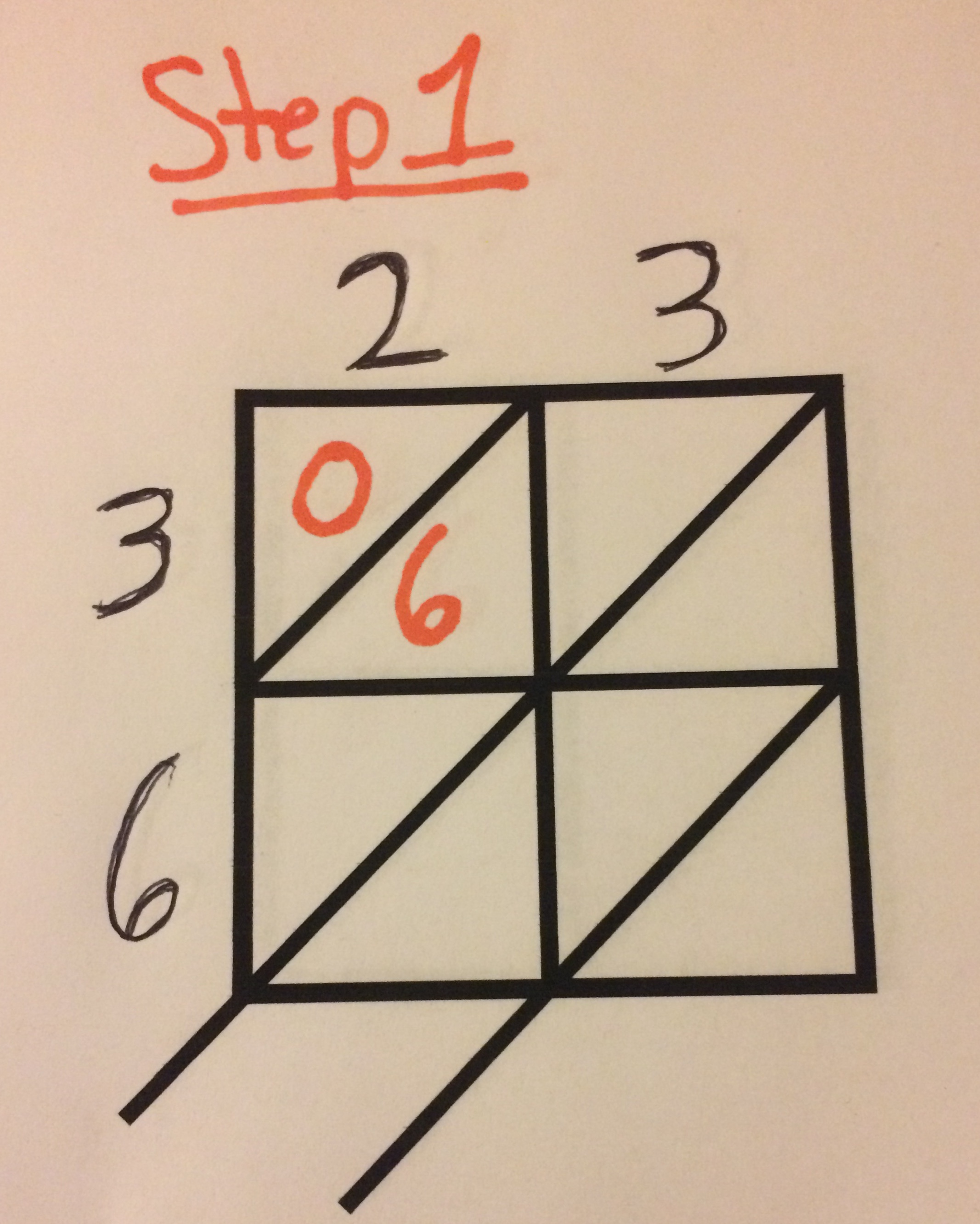
The first step is you have to have the lattice built. You create this by creating a box and dividing it into smaller boxes. Since we are focusing on multiplying two-digit numbers we need to create a box and divide it into four smaller boxes by drawing a line horizontally and vertically. Then you will divide all the boxes diagonally. (See the picture above for an example)

Then you will multiply the 1st digit in the 1st number with the 1st digit in the 2nd number. The tens digit goes above the diagonal line the one’s digit goes below the diagonal line. If there is no tens digit in the answer you put a zero above the diagonal line.

For instance, in the example above. When multiplying 23 times 36. You first multiply 2 times 3 which equals 6. Then since there is no tens digit in 6. You put a zero above the line and a 6 below the line.

Lattice Multiplication Step By Step: Step 2

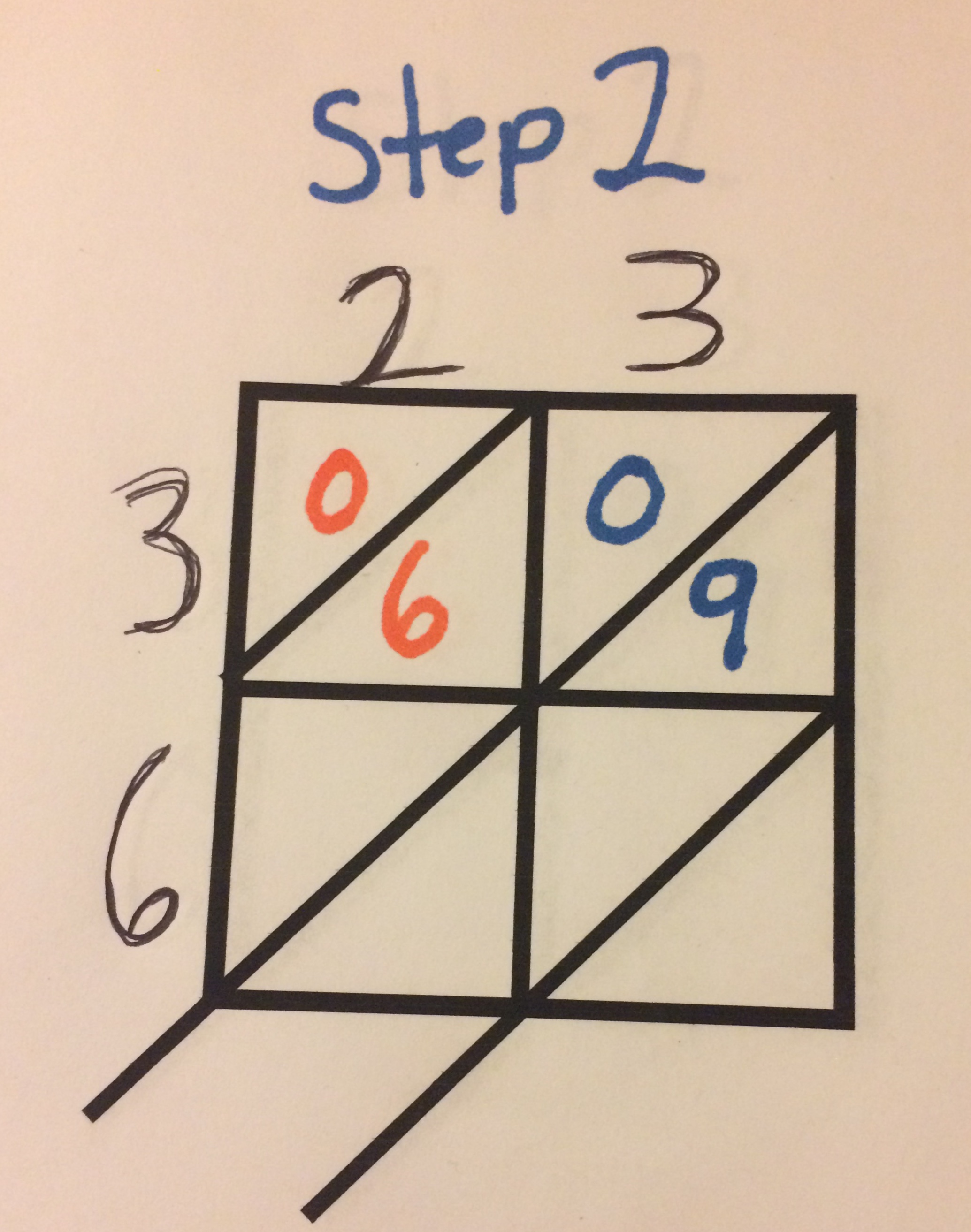
For our next step, you repeat the process with the 2nd digit in the 1st number and the 1st digit in the 2nd number. So in 23 times 36. In step two you will multiply 3 and 3 to get 9. Since there is no tens place again. The 9 goes below the diagonal line and a zero is placed above it.

Lattice Multiplication Step By Step: Step 3

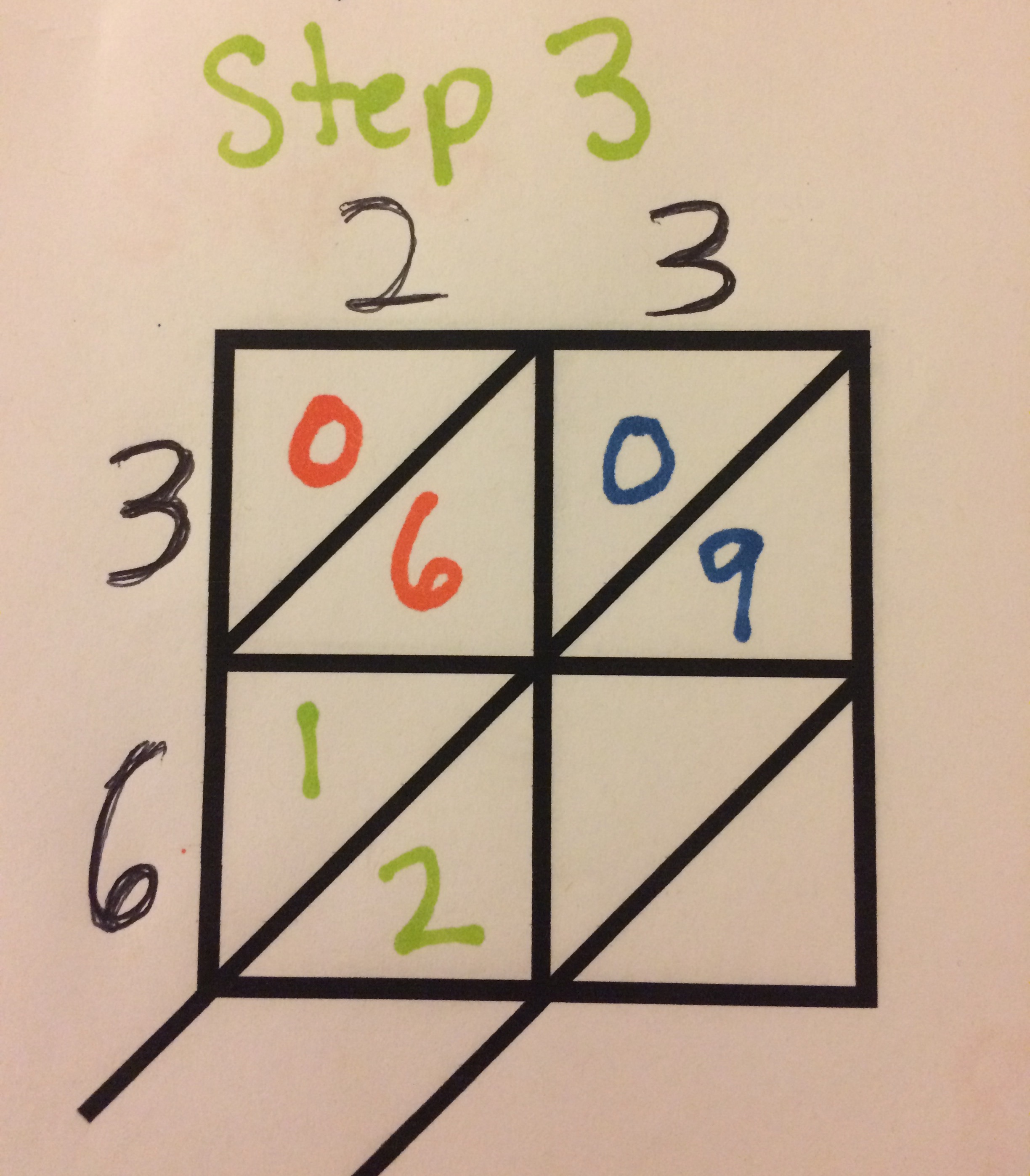
Step 3 repeats the same idea with the 1st digit in the 1st number and the 2nd digit in the 2nd number. In the example above this means multiplying 2 and 6 which gives you 12. This time there is actually a tens place, therefore, a 1 goes above the diagonal and the 2 goes below the diagonal.

Lattice Multiplication Step By Step: Step 4

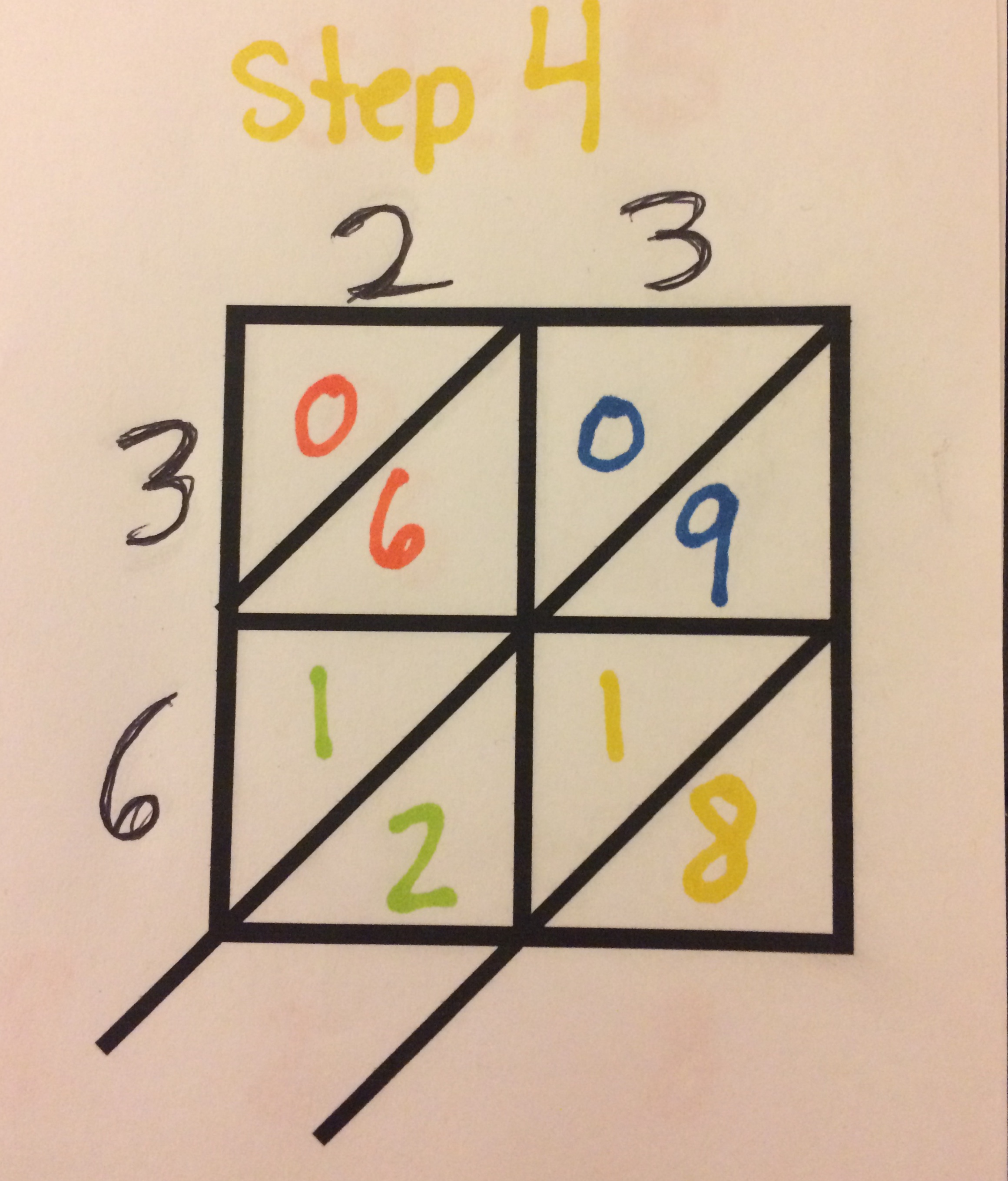
Lastly, you repeat this process with the last two numbers. The 2nd digit in the 1st number and then the 2nd digit in the 2nd number. So 3 times 6 equals 18. Therefore, the 1 goes above the line and the 8 goes below the line.

Lattice Multiplication Step By Step: Step 5

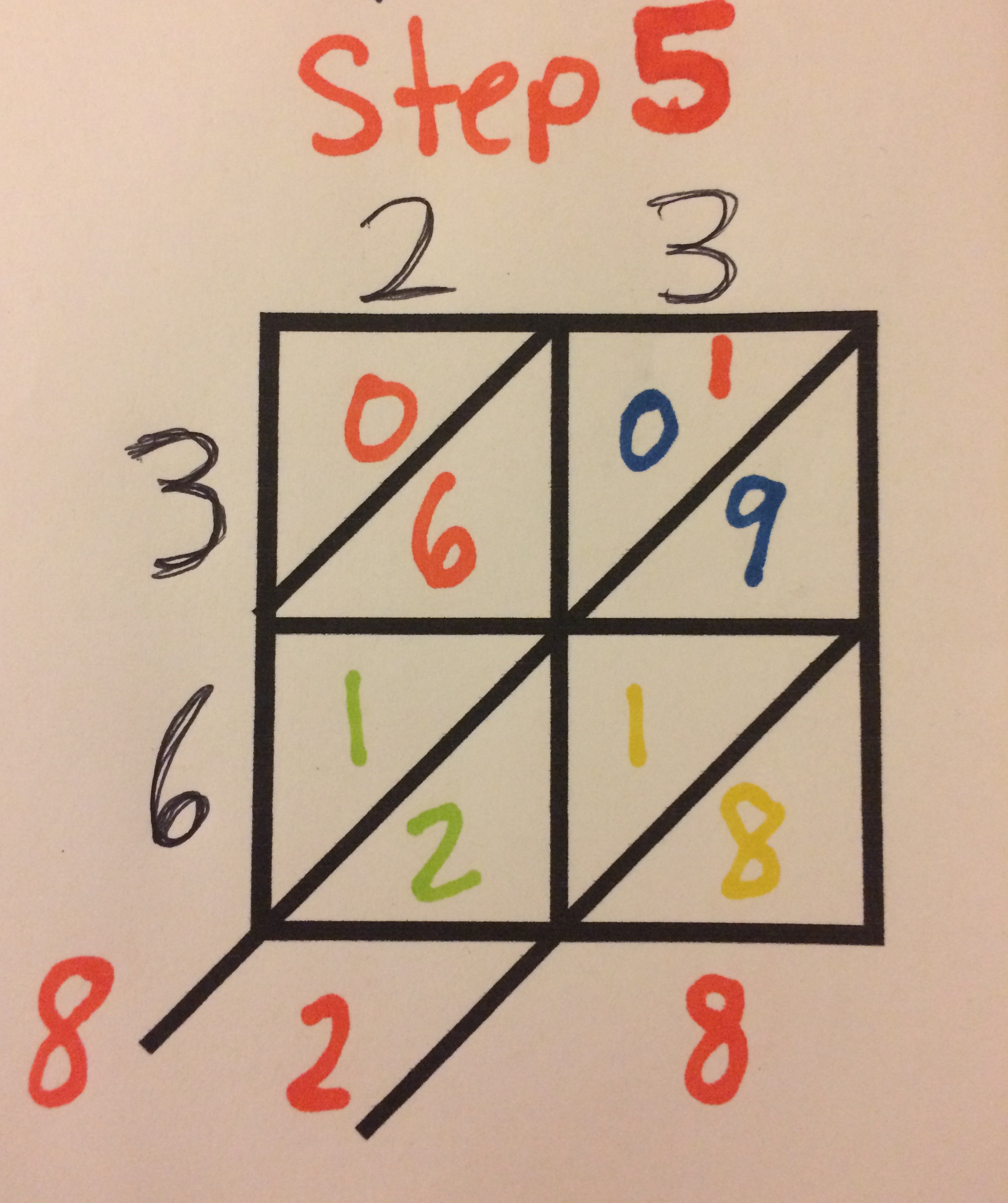
So now that we have the lattice full we have to actually add the numbers together. How we do this is we add along the diagonals. So in the example above you start in the bottom right, the 8 is by itself so it comes down. Then you move to the next diagonal. 9+1+2=12. The two comes down and you carry the 1. Then the next diagonal is 1+0+6+1=8. Then the last diagonal is a zero. Therefore, our answer is 828.

Also, for those of you who would do better seeing this broke down here is a video of the method.

Want to Read More?!?!

5 Math Games to Make Learning Fun

Stop the “Reading is Boring” Excuse

The One Way to Help Your Child Succeed In School

Lattice Multiplication Worksheet

So now that you know the process a little better you may want to actually do this and teach your students. I have uploaded a step by step visual guide of this lattice multiplication to my freebies page to grab access to the page sign up to become a subscriber in the form above and below.

However, if you want a full set of worksheets that includes 3 pages of pre-made problems as well as a couple pages of premade lattices for students to fill in their own problems. Head over to my Teachers Pay Teachers store.

This worksheet will be very helpful for your middle to upper elementary children especially if they are visually oriented.

I love this method because I have seen many kids thrive under it. There are many kids that the traditional methods just don’t click with, and to see their eyes light up when they understand how to multiply under this method is so amazing. It seriously makes my job one of the best jobs in my mind. I hope your kids will benefit from this method as much as I have seen my students benefit.

If you enjoyed this article please share it so that others can benefit as well. A great way to do that is Pinterest